为什么学习不仅要结果,更要过程?
两个人都能解决同一个问题,但他们用的方法可能不同。有些解决问题的方法容易应用到解决其他问题上,另一些方法就不容易。因此,我们不仅要关心问题的解决结果,而且要关心解决问题的方法,不同的方法意味着不同的知觉、记忆,应用了不同的技能和策略。
心理学家卡托纳曾经做过一个这样的实验。只允许受试者动三根火柴把下图中的五个方块变成四个等大的方块。他给三组受试者不同的指导:
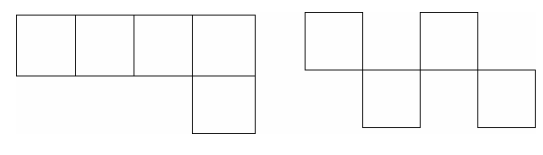
(1)机械学习:告诉受试者移动哪几根火柴,让他硬记,而不加任何解释。
(2)给予解释:告诉受试者其有16根火柴,如果每根都成为方块的一条边,那就可以组成四个方块。在这里16根火柴之所以能组成五个方块,是由于有些火柴作了两个方块的公用边。要解决这个问题应使每根火柴只起一条边的作用。这个解释容易使人迷惑,因为应该挪动的三根火柴并不是起公用边作用的,而是起单条边作用的火柴。但是挪动了这三根起单条边作用的火柴可以消除起公用边作用的火柴。
(3)给予暗示:启发受试者说“因为五个方块在一起太挤了,所以才使得某些火柴起到双重功能的作用(公用边)。要解决这个问题,就要使这些方块分散开”。
受试者所用的这三种方法都不需要很多的短时记忆。虽然三种方法的策略不同,但受试者最后都能解决问题。
然后,卡托纳把问题稍微做了修改,如下图所示。
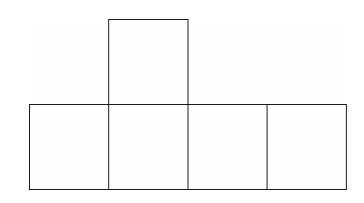
在这种情况下,先前用机械学习方法解决问题的受试者,现在就遇到了很大的困难,而用后两种方法的受试者,特别是用第三种方法的受试者,却很容易解决问题。
机械学习的方法是无意义的学习,记忆没有多余性,学会的内容难以保持。至于为什么第三种暗示启发的方法要比第二种解释的方法效果好,可能是后者告诉了受试者火柴的单功能与双功能问题,反而把受试者的思路引向火柴的功能本身,而不去注意最后的目标。暗示启发的方法最有效,当告诉受试者方块太集中,需要散开,就是说需要破坏原有的结构,移动几根火柴使各个方块离开远一些,这样就接近达到最后的目标。
用不同的学习方法会得出十分不同的结果。我们不仅要学会解决问题,而且要学会使用较好的方法解决问题。如果一个人总使用机械学习方法,他会认为自己学会了,以后习惯用这种方法,实际上他是很难把知识运用到新的情境中去的。
问题解决的途径
人在解决问题的时候,可以采取不同的途径或方法。人们可以用随机尝试的方法,经过多次试错,最后得到答案;也可以根据一些规律,或在经验中已经证明是行之有效的方法来解决问题,而且把尝试的次数减到最少。另外还有其他解决问题的方法,下面介绍的就是其中的几种。
假设—检验法
现在以解密码算术题为例,来说明解决问题所采取的两种不同的途径。下面这个密码题的上、中、下三行各是一个人名:
DONALD
+GERALD
ROBERT
已知:D=5
任务要求:
(1) 把字母换成数字;
(2) 字母换成数字后,下面一行数字答案必须等于第一行与第二行数字之和。
这个问题比较困难,因为解题共有300万个可能的尝试,即10!=3×106。如果我们知道了一个线索:D=5,则各种可能的尝试减为9!=3×105个。
一种解决问题的方法是,每个数字任意给一个英文字母,进行计算,当发生矛盾时就把数字和字母之间的对应关系再做新的安排,重新计算。用这种随机尝试的方法需要3×105次才能得到正确答案。
另一种方法是,系统地从右向左,利用解决问题中所得到的知识来做。因为D=5,就可以知道T=0。由于我们知道了T和D的数值,尝试的范围就缩小了。最右边的一列解决后,接着再看其左边的一列。用这种方法反复试验,经过许多组合,可以得出一个正确答案。
然而,以上两种先提出假设再进行检验的方法(假设检验法)都不是有效的方法。在实验室中采用这两种方法的人往往都失败了。
选择性搜索
解决密码算术题的有效的方法是先找出可能性最少的一列,从中获得最多的信息;再利用加法中的某些规则去进行推理,从而找到正确答案。这种方法叫作选择性搜索或启发式搜索。
所谓可能性最少的那一列,就是限制性最多的那一列。
能够解答这一问题的受试者几乎都用了这种方法。在解决这个问题时,受试者的主要思路只有几条,只利用了6个可能性,而不是用30多万次的尝试。由此可见,由于采取了这几条主要的思路,就可以排除大量的尝试,达到解决问题的目的。
这种有效的方法就叫作启发式搜索。
爬山法
爬山法的基本思想是设立一个目标,然后向目标方向运动,逐步逼近目标。这就像爬山一样,如果在山脚下,要想爬到山顶,就得一点点地往上走,一直走到最高点。有时爬山法得先上矮山顶,然后再下来,重新爬上最高的山顶。因此,爬山法只能保证爬到眼前山上的最高点,而不一定是真正的最高点。
在一些经典的用人或动物做受试者的心理学实验中,除了设立目标之外,还在目标与受试者之间加入一个障碍,使受试者不能直接达到目标,如下图所示:
在目标与受试者之间加入障碍

在这种情境下,受试者要花费相当长的时间去克服困难,找到绕过障碍的方法,有时甚至要倒退才能绕过障碍物达到目标。这就相当于在爬山法中经过曲折的途径而达到最高的山顶。当然,爬山法在我们日常生活中也是有用的方法,不少实际问题都是靠这种方法解决的。
总结以上几种解决问题的方法,我们看到,初次接触一个问题的人之所以能够解决这个问题,就在于他可以把过去已经掌握的一般解决问题的方法应用到新的情境中去。心理学的智力测验并不是测受试者已经知道的东西,而是测他将过去掌握的一般知识应用到解决测验的项目中去的能力。
我们通常把不依赖已有的具体知识来解决当前问题的方法称作弱方法。前面提过的假设检验法就是弱方法。用假设检验法解决密码算术题时,任意给每个密码设想一个数,然后再进行检验,这里并没有运用已有的具体知识。爬山法也是弱方法。这些方法是最粗糙的方法,其效率是很低的。如果是利用已有的有针对性的知识来解决某个问题,这就是强方法。例如,让受试者找X、Y的函数关系,如果他没有微积分知识,就得一点一点地试,使X值逐渐增大,看Y的变化,一直到找到最高点,得出结果。这就是弱方法。如果他已经具备数学方面的知识,那么就可以利用微积分把最高点定为0,这就是强方法。选择性搜索是利用过去已有的知识经验,有针对性地提出假设,然后再进行检验得出结论。这是有效的解决问题的方法,是一种强方法。在解决某个问题的时候利用强方法,是非常重要和有效的。
手段目的分析法
人类解决问题有一个很重要的方法,即手段目的分析法(means-end analysis)。这种方法的复杂性在于我们现有的状态与目标之间会有多种差异,而不是一种差异。我要去听课,却忘记带本子和笔,要解决本子和笔这两个差异,才能在课堂上记笔记。我发现身上带着几角钱,于是就产生了买纸和笔的活动。但是,买了纸后再买笔,钱又不够用了,这时我就发现自己做错了,于是又把纸退了,用退了纸的钱去买笔,买过笔再用剩下的钱去买纸。解决问题中出现多种距离和差异的情况是常见的。我们解决了第一步问题,然后再解决第二步问题,可是在解决第二步问题时,第一步问题又出现了。因此,为了更好地运用手段目的分析法解决问题,就需要有解决问题的结构。
例如,玩魔方时,我们可以先把其一面完全变成单色,比如先把第一面变成白色,然后再想办法把其他几面分别变成红的、黄的等等。这里的问题是,在变第二面时不能破坏第一面;变第三面时不能破坏第一、第二面。我们也可以用手段目的分析法来解决这个问题。使用这种方法我们在变第二面时,可以破坏第一面,但只是暂时的,还要很快地恢复第一面的全白色。事实上,这种一面一面地解决的方法不一定是最好的方法。这是个慢的方法。我们最好能用更简单的方法,从整体上来考虑如何把魔方恢复为六面单色。为了学会这种整体性的动作,或者说是“宏观动作”,我们不如买一本魔方解答指南一类的书,从中学会这种“宏观动作”。这种“宏观动作”不是原来的一个动作,而是一系列的动作,包括暂时破坏某一面又将其恢复的过程。
这种解魔方的宏观方法,平时我们就称其为“计划”。
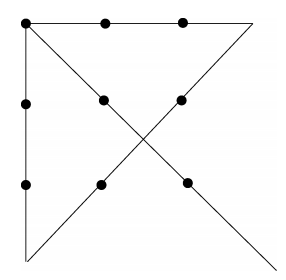
心理学教科书中时常引用的画4条直线通过9个点的问题图(见下图),看起来容易,做起来却很困难。这个题可采取的搜索树的分枝并不多,但人们考虑问题时却往往忽略某种可能性,即为了解决这个问题,解题人所画的直线一定要超出这9个点所形成的正方形,否则就无法解决。尽管出题的人并没有限制解题者,也没有禁止他超越正方形,但解题者却常常自己限制了自己,他没有考虑到利用某种算子来解题,因而使问题变得很难。
书生和野人的问题也属于这类问题。题目是这样的:有三个书生和三个野人走到河边,河里只有一条渡船,而且至多只能乘两人。现在问应该怎样使用这条船将三个书生和三个野人渡到对岸去。解决这个问题有一个条件,即无论在船上还是在岸边,书生的人数都不得少于野人,否则书生就要被野人吃掉。解决这道题的方法分如下几步(见下图):
(1)两个野人先过河。
(2)一个野人划船返回。
(3)然后再过去两个野人。
(4)一个野人又划船返回。
(5)两个书生一起过去。
(6)为了进一步解决问题,现在要走关键的一步,就是要有一个书生和一个野人划船回来。只有想到这一步,以后各步才能顺利进行。
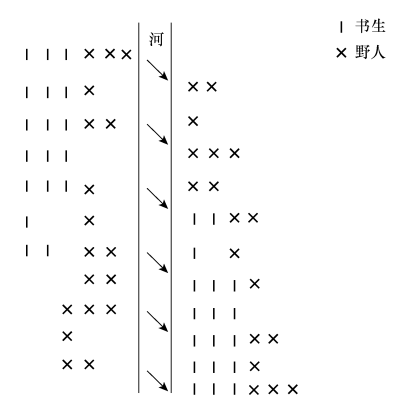
这个问题是不容易解决的。一位大学教授在一刻钟内也常常解决不了,除非他能认识到,尽管目的是尽量向对岸摆渡更多的人,使他们全部过去,但是也允许两个人划船回来,问题才容易得到解决。这样的问题的搜索空间并不太大,关键是在第六步两个人划船回来。由于一般很难想到两个人划船回来这一步,所以问题就变得很难。
所以,有的问题的困难不在于问题本身,而在于人们思维习惯。 考虑问题时忽略了某种可能性,没有想到某一种似乎背离目标但实际是接近目标的方法,或者不能很好地把问题形象化都会导致问题变得难以解决。

- 来源:《认知:人背后的思维与智能》作者:赫伯特·西蒙,中国人民大学出版社,2020年1月出版。本书是人工智能之父、迄今唯一同时获得图灵奖和诺贝尔经济学奖的科学天才赫伯特•西蒙的经典作品。书中为我们介绍了人的认知特点,包括注意、联想、记忆等方面,分析了解决问题的途径和策略。点击→《认知:人背后的思维与智能》,立即购买。







暂无评论,点击讲两句