系统思考是VUCA时代的必备生存技能,因果回路图是系统思考的一个基础性工具,掌握了它,系统思考就可以从“虚”变“实”,我们就更有可能解决复杂问题,做出睿智决策,在VUCA时代从容生活。
本文内容分为5部分:
1、什么是因果回路图
2、如何辨认回路的特性
3、增强回路
4、调节回路
5、五个步骤绘制因果回路图
下面我们一一来详述。
1、什么是因果回路图
《如何系统思考》中说,因果回路图是系统思考的“新语言”,这个描述比较抽象,看了也不知道因果回路图到底是什么。我来发个图片,请大家先看个样子。
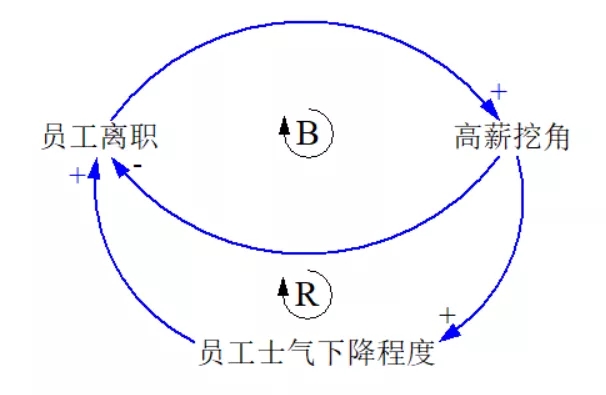
这张图是《如何系统思考》第4章,员工离职案例对应的因果回路图。看了这个图,我们对因果回路图会有个具体的印象,知道它长什么样子。然后我们再来看《如何系统思考》这本书给因果回路图下的定义:因果回路图是以因果关系链路的形式来描述影响系统行为的结构。
在这个定义中,有三个关键概念:
1、因果关系链路 2、回路 3、系统的结构
搞明白它们,就知道因果回路图是什么了。
1.1 因果关系链路
我们先看因果关系链路。它大概长这个样子。

因果关系链路,由具备因果关系的变量和它们之间的连接构成。上面的图片中,ABCD都是变量,蓝色的弧形箭头和它旁边的加减号,代表连接。
变量是一个系统中的实体、属性或要素,它们可能影响其它变量,也可能被其它变量影响。因果关系链路上的两个相邻的变量之间,必须是因果关系。
变量A和变量B,A的变化能够直接或间接引起B的变化,A和B之间就存在因果关系。比如天冷了加衣服,气温和加衣服之间,就有因果关系。
如果A变化时B也变化,但B的变化不是由A引起的,那A和B之间就是相关关系,而不是因果关系。
举个例子,夏天的时候,冰淇淋消费量越多,犯罪率就越高。冰淇淋消费量和犯罪率是正相关的,但并不意味着冰淇凌消费的增多导致了犯罪率的上升,更不可能通过减少冰淇凌的销售来降低犯罪率。冰淇淋消费量和犯罪率之间没有因果关系。
因果关系链路上的两个变量之间,必须存在因果关系,不能是相关关系。
连接反应两个变量之间的关系和变化方向,用有向箭头和极性来表示。如下图所示:
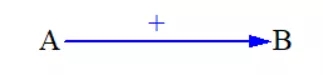
这个图片上,变量A在箭头起点,表示原因,变量B是在箭头结尾,表示结果。箭头上的+号,表示A和B是同向变化。这四个元素组合在一起,形成的就是一个同向连接,意思就是,A影响了B或A导致了B,并且A增B增,A减B减。
举个例子,比较容易明白,产品的销售和收入之间,就是同向连接,销量越多,收入越高,销量越低,收入越少。

除了同向连接,还有一种连接,如下图所示:

这个图片上,变量A在箭头起点,表示原因,变量B是在箭头结尾,表示结果。箭头上的-号,表示A和B是反向变化。这四个元素组合在一起,形成的就是一个反向连接,意思就是,A影响了B或A导致了B,并且A增B减,A减B增。
举个例子,在其它情况都不变的前提下,成本和利润之间,就是反向连接。成本越高,利润越低,成本越低,利润越高。

1.2 回路
所谓回路,指的是从一个因素出发,沿着箭头方向,经过一系列因果相互作用,又反作用于自身的循环。
回路有两个特点:
1、闭合
2、单方向循环
看下图,比较一下,大家就明白什么是回路了。
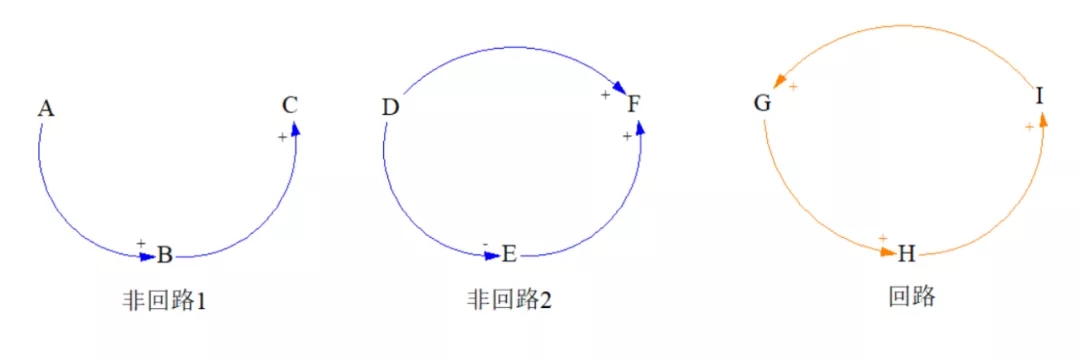
如图所示,最左边的链路不是回路,因为它不闭合。中间的也不是回路,D指向F,E也指向F,箭头有两个方向,不是单方向的。只有最右面的链路,才是回路。
1.3 结构
接下来我们说下系统的结构。系统思考中有个冰山模型,如下图所示:

因果回路图要描述的结构,就是冰山模型中最底层的这部分,指的是系统中的关键变量和它们之间的联系方式,它会影响上面的模式和事件。
好了,到这里,我们就介绍完了因果回路图,因果回路图就是用变量、连接和各种因果关系链路组成的,来描述系统结构的图表。
下面是一个简单的因果回路图。
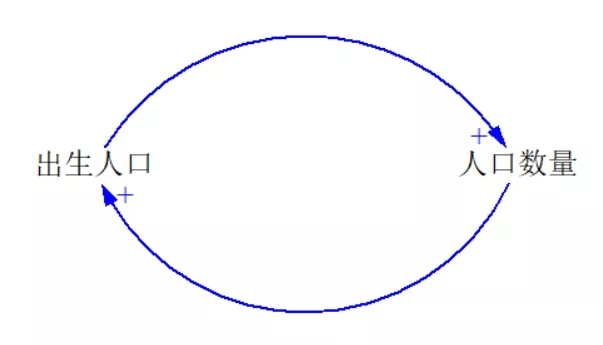
这个因果回路图表示的是一个简化的人口模型,出生人口增多,会导致人口数量增多,人口数量增多,又会导致出生人口增多。
我刚给的是一个简化的系统结构,实际运用中,我们接触到的系统往往比较复杂,它的结构,往往需要由多个因果回路组合在一起才能表示。
2、辨认回路的特性
刚才我们介绍了什么是因果回路图。不同的因果回路,效果不同。有的因果回路,可以增强系统中事物的原有变化态势,这类回路叫增强回路(Reinforcing Loop,在因果回路图上以字母R指代)。有的因果回路,会自我调整,抵消并阻止变化,这类回路叫调节回路(Balancing Loop,在因果回路图上以字母B指代)。
所有的系统,不论多么复杂或多么简单,都可以用增强回路和调节回路组成的网络来表示。
不同类型的回路,可以从不同的侧面帮助解决问题,所以我们有必要辨认系统中的回路哪些是增强回路哪些是调节回路。
辨认的方法有两个。
一个是基于动态系统的基本行为模式来判断。
按照系统思考的原理,结构影响行为,动态系统的行为模式是由底下的结构决定的,不同的结构会导致不同的行为模式。所以我们可以根据动态系统表现出来的模式,来反推系统中的结构。
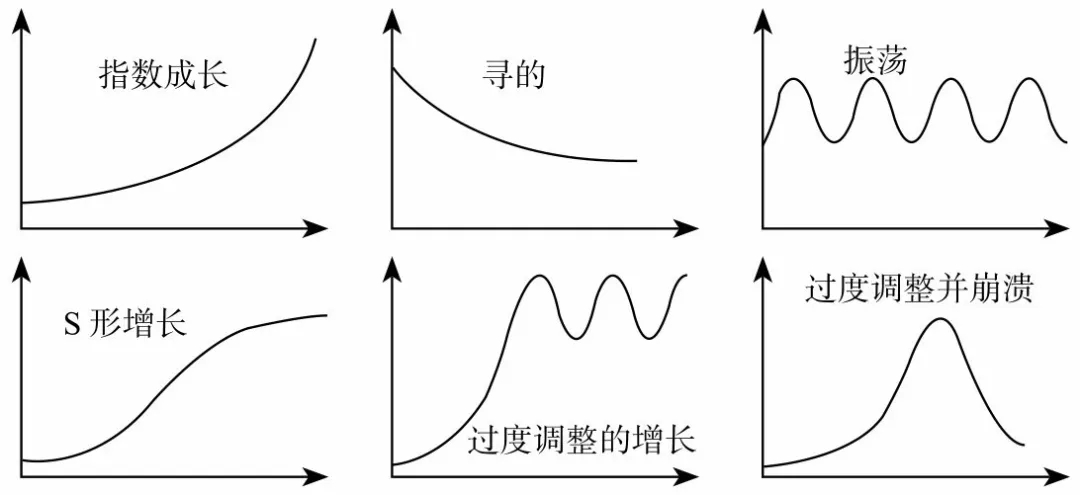
要做到这点,一方面要理解6种常见的行为模式和对应的系统结构,另一方面,还不要在实践中积累经验。这是我们系统思考修炼的一个目标,今天我们先跳过这种方法,来说第二种方法。
第二种辨认回路特性的方法是根据回路的结构特性来判断。
这种方法要求我们先把系统的因果回路图画出来,然后去数一个因果回路中反向连接的个数,个数为偶数,这个回路就是增强回路;个数为奇数,这个回路就是调节回路。
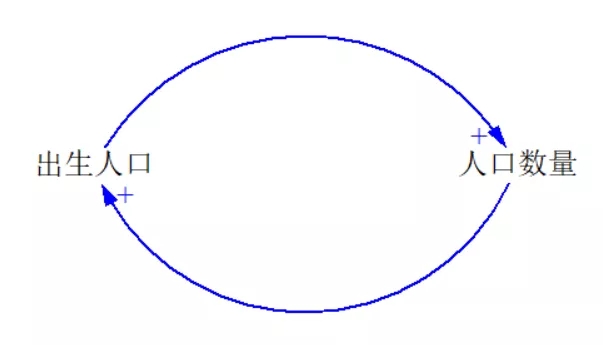
请你根据这个因果回路中反向连接的个数是奇数还是偶数,判断一下它是增强回路还是调节回路。(测试1,答案在文章末尾)
有没有注意到,这个回路中没有反向连接。没有反向连接的回路,反向连接个数为0,是偶数,回路是增强回路。
再来看员工离职的因果回路图。
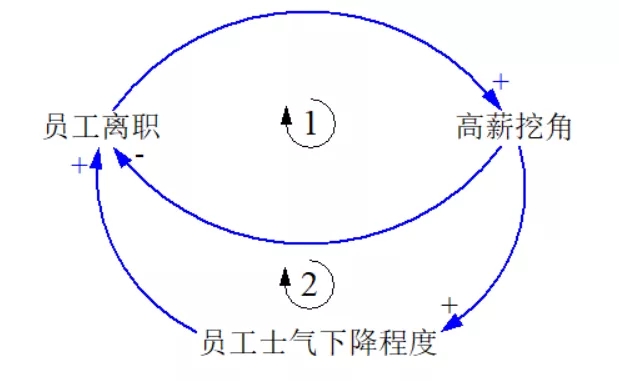
如上图所示,上面有两个因果回路。我标注了序号,请你判断它们是增强回路还是调节回路。(测试2,答案在文章末尾)
刚刚是两个比较简单的因果回路图。现在我们来看一个复杂的,有挑战了哦。
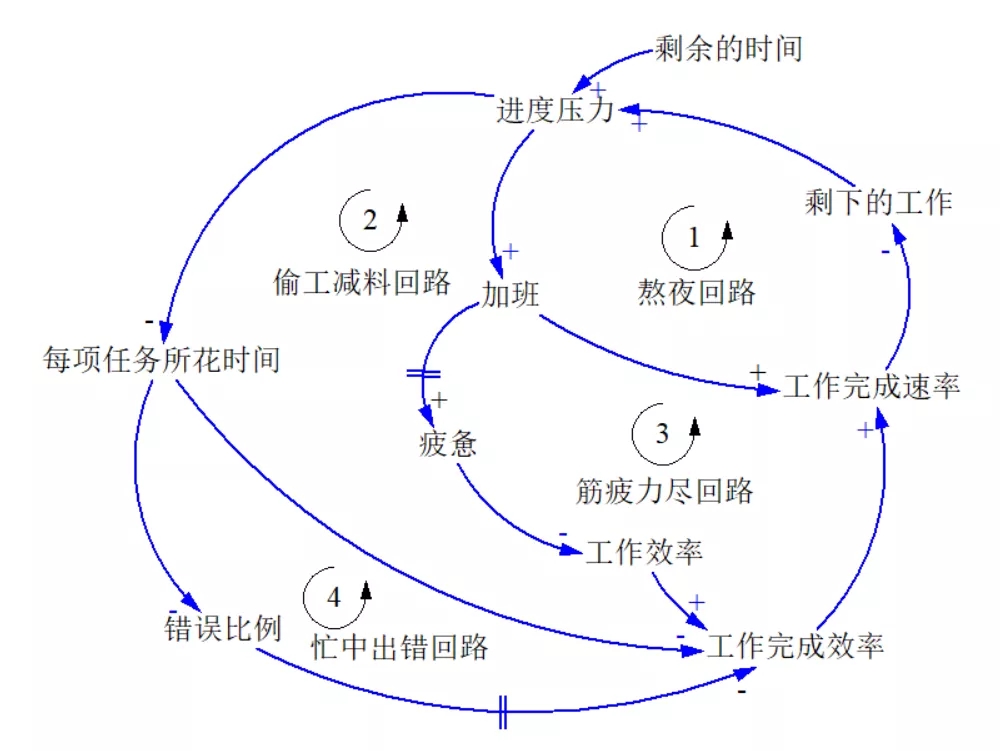
在这个因果回路图上,有4个回路,我标注了序号,请你辨认一下,看看它们都是什么回路。(测试3,答案在文章末尾)
好了,关于辨认回路特性,我们先讲到这里,现在大家知道因果回路有增强回路和调节回路这两种,也学会了怎么辨认它们,接下来我们来进一步学习增强回路和调节回路。
3、增强回路
咱们先看增强回路。
先举个例子。破窗效应,很多小伙伴都听过,它说的是这么一个现象。
如果有人打坏了一幢建筑物的窗户玻璃,而这扇窗户又得不到及时的维修,别人就可能受到某些示范性的纵容去打烂更多的窗户。久而久之,这些破窗户就给人造成一种无序的感觉,结果在这种公众麻木不仁的氛围中,犯罪就会滋生、猖獗。
破窗效应背后的因果回路图是这样的:
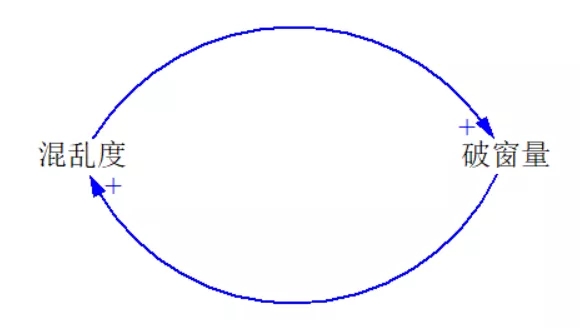
这是个增强回路,这个回路,对应的产生破窗效应的地区,混乱度会越来越高。这就是增强回路带来的效果,它会放大系统中事物原有的变化趋势。
如果系统中的事物原来是往好的方向变,在增强回路的作用下,就会越来越好;反过来,如果系统中的事物原来是往坏的方向变,在增强回路的作用下,就会越来越坏。
比如富者越富,背后的增强回路,会让富者的财富持续增长,越来越多。而相应的,穷者越穷,背后的增强回路,会让穷者的财富越来越少,甚至陷入破产。
增强回路,就是这样,具有自我增强的特点。
我再举个定投的例子,我们在投资基金时,一开始会买入一定的额度,过上一段时间,会获得红利,如果把红利拿来再投资,投资额就会增长,下次就能获得更多的红利……如此往复,就会形成一个良性循环,投资额就会越来越多。这样一个过程,其实背后就有一个增强回路,我画了对应的因果回路图,供参考。你也可以画自己的。
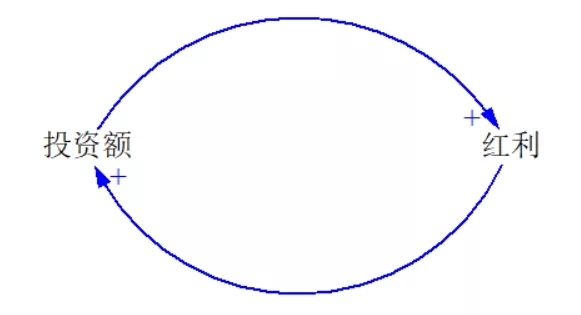
类似这样的增强回路,我们的生活中有很多很多,留意那些越来越好或者越来越坏的现象,留意那些良性循环或者恶性循环,往往你就能发现增强回路。
讲到这里,大家应该能理解什么是增强回路了。下面我们来做一个小练习,根据一段描述来画出问题被后的增强回路。
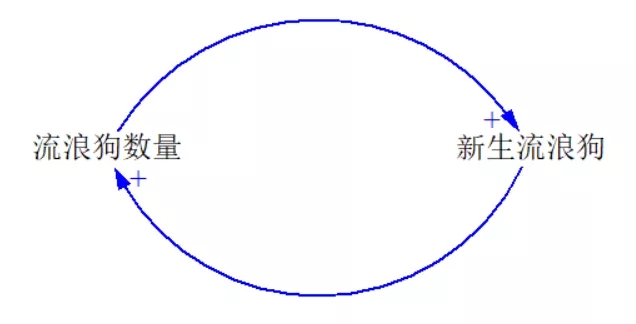
在一些大都市,一些宠物狗因各种原因被遗弃,成为流浪狗,由于其中一些没有采取绝育手术,因而繁衍出了一些“下一代”,而这些下一代本身就是流浪狗,等它们成年后又会繁衍出更多的下一代……一段时间以后,都市里流浪狗泛滥成灾。
(练习1,参考答案在文章末尾)
4、调节回路
刚我们讲增强回路时,说它可以放大系统中事物原有的变化趋势。但实际上,趋势不会一直增强。我们来看人口模型的增强回路。
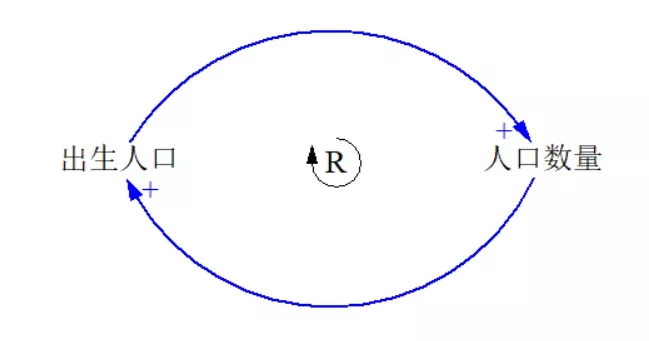
按这个增强回路,人口数量会越来越多,像我们国家,可能从8亿到10亿到20亿甚至更多。但实际上,人口数量并不会照这个模式发展。
为什么呢?
这是因为,任何一个增强回路,都不会独立存在。随着系统的运行,总会出现一些限制因素,限制原有趋势的发展,甚至逆转原有趋势。
比如人口系统,随着人口数量的增加时间的推移,死亡人口也会不断增加,导致人口数量下降,这就会抵消出生人口带来的人口数量增长,改变人口增长的趋势。
人口数量下降背后,有一个调节回路。如下图所示。
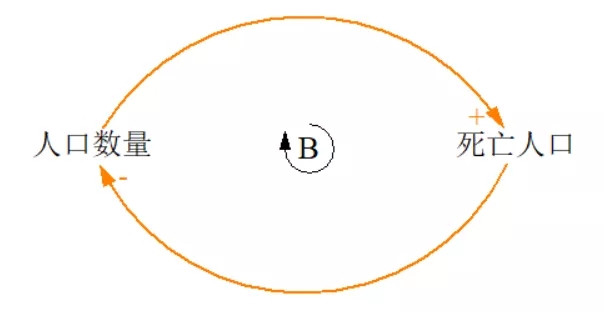
我们把人口数量下降和人口数量增加对应的两个因果回路放在一起,就组成了一个更符合人口模型的因果回路图。
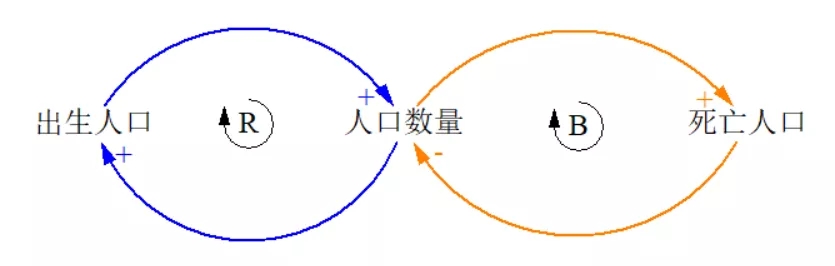
大家可以看下这个因果回路图,它是非常典型的,在我们生活中特别常见,被列为最常见的系统基模,名字叫作“成长上限”。
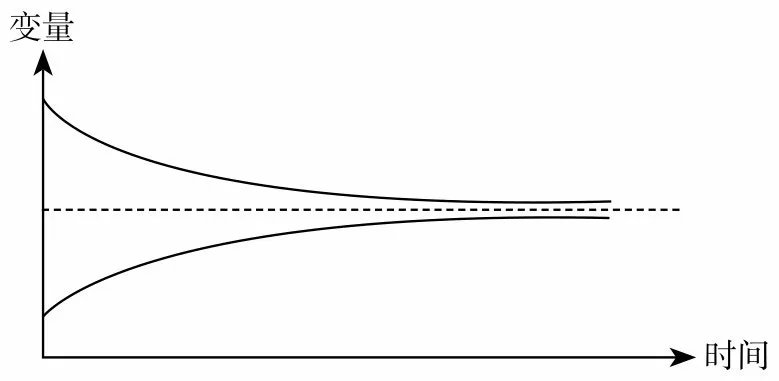
我们从人口模型这个例子中也可以看出,调节回路,具有自我调整的特点。它这种特点,在行为特性上,就表现出“向某个目标靠近”的特点,也就是寻的特点。假如系统中某个事物在开始时具有快速上升的趋势,那在调节回路的作用下,上升幅度就会越来越小。假如系统中某个事物在开始时具有快速下降的趋势,那在调节回路的作用下,下降幅度就会越来越小。我从《如何系统思考》中截取了一张图片,很好的描述了调节回路的这种行为特性。
我们来看个调节回路的例子。
一家西餐厅,环境优雅,服务体贴,在这里就餐过的顾客都愿意推荐这家西餐厅给朋友们,于是这家西餐厅的顾客越来越多,结果西餐厅服务不过来,服务质量开始下降,引起顾客不满,口碑变差,后面再来的顾客就会变少,当顾客少了之后,西餐厅的服务质量又上来了,口碑再次变好,又吸引了越来很多顾客前来就餐……事情这样循环下去,慢慢的,这家西餐厅的服务就会稳定在某个水平,客流也会稳定在某个量级。这家西餐厅发生的情况,后面就是一个调节回路。

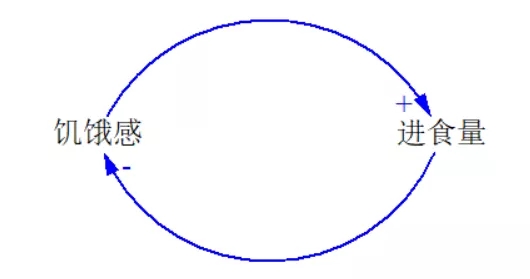
像这样的调节回路,生活中特别多,比如饥饿进食。
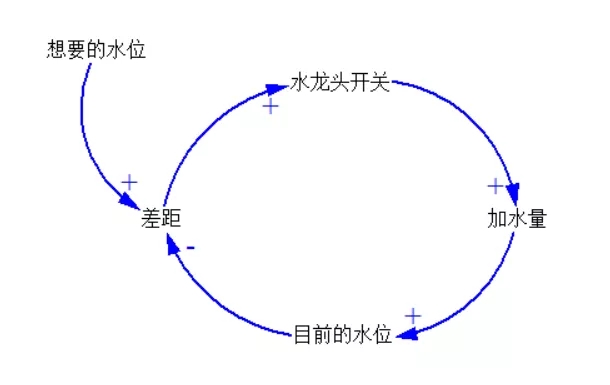
比如拿水杯到水龙头下接水。
还有,像空调的恒温效果,开车时的定速巡航,里面都有调节回路。
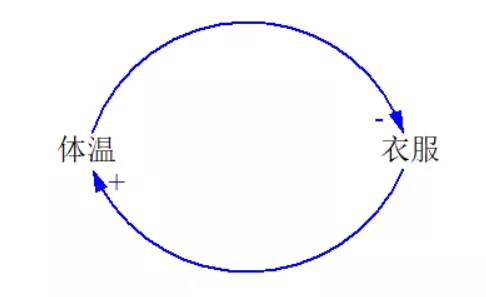
好了,讲到这里,大家应该能理解什么是调节回路了。下面我们来做一个小练习,请你画出“天冷加衣服”这个现象背后的调节回路。
(练习2,参考答案在文章末尾)
可能不少小伙伴会更喜欢增强回路,比如赚钱越来越多,自己越来越优秀,老婆越来越贤惠,老公越来越顾家,对应的,会不大喜欢调节回路,比如老公总是乱扔袜子你说一次好三天过了三天又恢复照常,但实际上,增强回路总是会有伴生的调节回路,调节回路是不可避免的,同时呢,调节回路也有很大作用。
第一个作用,就是帮我们发现系统隐藏的阻力因素,找到对应的解决策略。比如公司制定了一些新政策,一开始气象万千,后来执行不下去,这时就可以尝试找到调节回路,寻找破局的策略。
第二个作用,是平衡目标。比如我们前面举例的西餐厅,就可以根据调节回路,调整自己的目标,让餐厅的就餐人数,稳定在和服务能力匹配的水平上。
调节回路和增强回路组合在一起,构成的因果回路图,可以帮助我们更好的理解系统的结构,找到解决问题或实现目标的策略,所以我们不要厚此薄彼,要综合利用它们。
5、如何绘制因果回路图
前面我们介绍了什么是因果回路图,什么是增强回路,什么是调节回路,也给了很多例子,那有些小伙伴可能就有疑惑了:怎么绘制因果回路图呢?
5个步骤。
第1步,找到系统的关键变量。
对于增强回路,你要找到具备增长态势或有自我强化模式的变量。比如对于城市流浪狗增多这个现象,有增长态势的变量,就是流浪狗数量。比如破窗效应,有自我强化模式的变量,就是某个地区的混乱程度。
对于调节回路,你要找到系统想要靠近的目标或者被系统调节的变量。比如前面讲到的西餐厅,被调节的变量,是就餐人数。再比如,天冷加衣服,被调节的变量,是体温。
第2步,思考是什么因素,导致了这一变量的增长或衰减,它的驱动力是什么。
比如流浪狗增加,是新生流浪狗导致的。比如体温升高,是衣服导致的。比如餐厅客流下降,是服务质量变差导致的。
第3步,思考这个变量,会影响什么变量,它将驱动什么。
比如流浪狗,会影响新生流浪狗。比如体温升高,会导致你减衣服。
通过2、3两步的分析,你就能发现更多变量。
第4步,思考在这些变量之间,直接或间接地存在哪些相互影响或作用,把具有因果关系的变量,用同向或反向连接给连接起来,这样就能绘制出回路。
第5步,计算闭合回路上反向连接的数量,判断奇偶,判断回路是增强回路还是调节回路,标注到回路上。
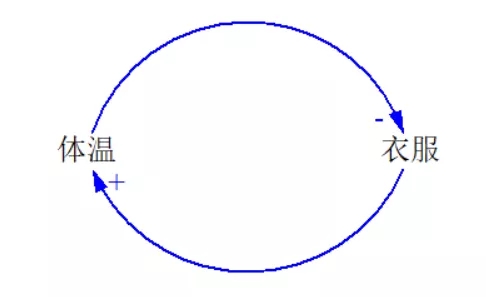
比如天冷加衣服,最终绘制成的因果回路是这样的:
因果回路图的绘制,需要反复的练习才能掌握,希望大家能在生活中多多观察,发现各种回路,抓住机会练习。在这里呢,也给大家留一个练习作为作业。
请阅读下面一段文字,绘制出因果回路图。
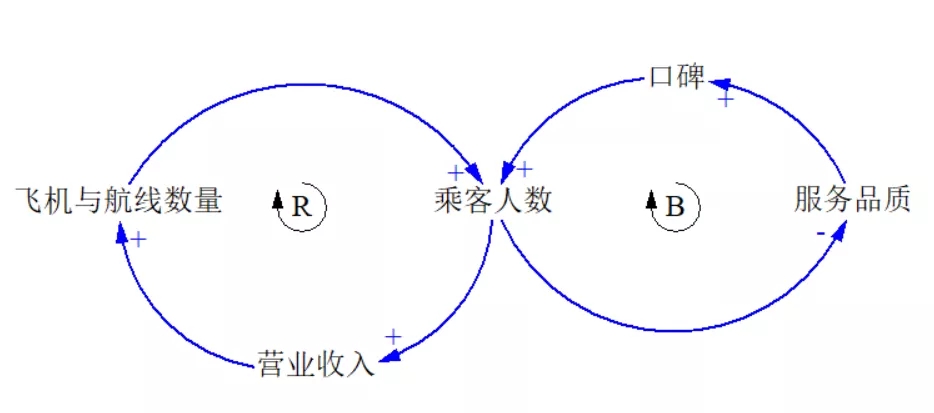
人民航空公司成立于1980年,定位于为美国东部的旅客提供价格便宜、高品质的空运服务,它在五年之中,成为全美第五大空运公司,取得了令人瞩目的成功。然而,到了1986年9月,人民航空被得克萨斯州的一家航空公司接手,单是当年前6个月就亏损1.33亿美元。
人民航空的急速成长在于其快速扩充飞机数量和航线,以及前所未有的低票价。由于创办人唐不二(Don Burr)极具个人魅力,他塑造了一种令人振奋的企业哲学,并率先采取了许多颇具创新性的人力资源政策,包括工作论调、社团管理、全面持股制以及扁平化管理等,员工的服务热情与质量也令顾客满意。这些因素使得乘客数量剧增,口碑效应为其带来了更多的乘客和可观的收入,使其进一步扩充机队规模。
然而,随着乘客人数的增多,超出了服务容量,使得服务品质开始下降,导致顾客流失。当竞争对手也开始降低票价时,人民航空的市场竞争力也随之下滑。
◇◇◇测试和练习答案◇◇◇
测试2,标号1的回路,是调节回路;标号2的回路,是增强回路。
测试3,标号1,2,是调节回路;标号3,4,是增强回路。
练习1,流浪狗增多问题后的因果回路,参考答案
练习2,天冷加衣背后的因果回路,参考答案








暂无评论,点击讲两句